Ricardo Kenji NawaI; Ada Clarice GastaldiII; Elisângela Aparecida Soares da SilvaIII; Viviane dos Santos AugustoIV; Alfredo José RodriguesV; Paulo Roberto Barbosa EvoraVI
DOI: 10.5935/1678-9741.20120040
ABSTRACT
OBJECTIVES: Cardiac surgery (CC) determines systemic and pulmonary changes that require special care. Awareness of the importance of respiratory muscle dysfunction in the development of respiratory failure motivated several studies conducted in healthy subjects to assess muscle strength. These studies were carried out by evaluating the maximal inspiratory pressure (MIP) and maximal expiratory pressure (MEP) values. This study examined the concordance among the values predicted by the equations proposed by Black & Hyatt and Neder, and the measured values in cardiac surgery (CS) patients.
METHODS: Data were collected from preoperative evaluation forms. The Lin coefficient and Bland-Altman plots were used for statistical concordance analysis. The multiple linear regression and analysis of variance (ANOVA) were used to produce new formulas.
RESULTS: There were weak correlations of 0.22 and 0.19 in the MIP analysis and of 0.10 and 0.32 in the MEP analysis, for the formulas of Black & Hyatt and Neder, respectively. The ANOVA for both MIP and MEP were significant (P <0.0001), and the following formulas were developed: MIP = 88.82 - (0.51 x age) + (19.86 x gender), and MEP = 91.36 - (0.30 x age) + (29.92 x gender).
CONCLUSIONS: The Black and Hyatt and Neder formulas predict highly discrepant values of MIP and MEP and should not be used to identify muscle weakness in CS patients.
RESUMO
OBJETIVOS: A cirurgia cardíaca (CC) determina alterações que demandam cuidados específicos no pós-operatório, incluindo as alterações pulmonares. A consciência da importância da disfunção da musculatura respiratória na insuficiência respiratória motivou o desenvolvimento de diversos estudos da força muscular em indivíduos saudáveis. Esses trabalhos utilizam valores de pressão inspiratória máxima (PIMÁX) e pressão expiratória máxima (PEMÁX). O presente estudo avaliou a concordância existente entre os valores preditos pelas equações propostas por Black & Hyatt e Neder et al., com valores observados em pacientes submetidos à CC.
MÉTODOS: Os dados foram coletados das fichas de avaliação pré-operatória. Para a análise estatística verificou-se a concordância existente entre os valores preditos e observados pelas as equações de Black & Hyatt e Neder et al., sendo utilizado o coeficiente de concordância de Lin e o gráfico de Bland-Altman. Posteriormente, os dados foram submetidos à regressão linear múltipla e análise de variância, para proposição de novas fórmulas.
RESULTADOS: Para PIMÁX, observou-se fraca concordância de 0,22 e 0,19 e para PEMÁX, 0,10 e 0,32, respectivamente, para as fórmulas de Black & Hyatt e Neder et al. Os valores da ANOVA para PIMÁX e PEMÁX, foram significativas (P<0,0001), permitindo propor as seguintes fórmulas: PIMÁX = 88,82 - (0,51 x Idade) + (19,86 x Sexo), e para PEMÁX = 91,36 - (0,30 x Idade) + (29,92 x Sexo).
CONCLUSÃO: As fórmulas de Black e Hyatt e Neder et al. predizem valores de PIMÁX e PEMÁX discrepantes, não devendo ser utilizadas para identificar fraqueza muscular em pacientes submetidos a cirurgia cardíaca.
CABG: Coronary artery bypass graft
CI: Confidence interval
CPB: Cardiopulmonary bypass
CS: Cardiac surgery
FAEPA/HCFMRP/USP: Foundation for Education, Research and Assistance Support (FAEPA), Faculty of Medicine of Ribeirão Preto Clinical Hospital, University of São Paulo (FAEPA/HCFMRP/USP), SP, Brazil.
FAPESP: Foundation for Research Support of the State of São Paulo (FAPESP)
LB: Lower bound
MEP: Maximal expiratory pressure
MIP: Maximal inspiratory pressure
PEMÁX: Pressão expiratória máxima
PIMÁX: Pressão inspiratória máxima
RV: Residual volume
TLC: Total lung capacity
UA: Upper airway
UB: Upper bound
VT: Tidal volume
INTRODUCTION
Cardiac surgery (CS) induces systemic changes, including pulmonary changes that require specialized postoperative attention. In recent decades, the number of patients with cardiovascular diseases that require surgical intervention has increased significantly. In adults, the most frequent indications for CS are heart valve diseases and coronary artery disease. Although considered safe, these surgeries are not free from complications; CS has an incidence of postoperative complications of approximately 5% [1]. Lung changes are the most frequent complication, occurring in up to 70% of cases and are responsible for atelectasis and pneumonia (24.7%) and hypoxemia and pleural effusion (47.5%) [2,3]. The respiratory muscles play a key role in the maintenance of the ventilation process. Therefore, recognizing patients with preoperative respiratory muscle weakness identifies those at increased risk of postoperative complications [4].
The effect of age on respiratory muscles cannot be ignored; muscle strength of the peripheral muscles, as well as the respiratory muscles, reduces with advancing age. In preparing patients for surgery, the detection of decreased respiratory muscle strength during the physiotherapy assessment prior to CS leads to early intervention and optimization of a program to strengthen the respiratory muscles. Like the integrated index (index of rapid shallow breathing index and CROOP), rates of respiratory muscle pump function, represented by the measurement of maximal inspiratory pressure (MIP), are widely used in clinical practice. The instruments can predict weaning success in patients undergoing mechanical ventilation, and assessing the performance of respiratory muscles is a crucial decision point for initiating weaning.
Awareness of the importance of respiratory muscle dysfunction in the contribution of respiratory failure led to the development of several studies conducted in healthy subjects in order to indirectly assess muscle strength by evaluating maximal inspiratory pressure (MIP) and maximal expiratory pressure (MEP) values. There are several equations available in the literature to assess MIP and MEP, but two are widely used; the formulas proposed by Black & Hyatt [5] and Neder et al. [6] were established using pressure values measured in normal populations. Thus, this study examined the agreement between the maximal static respiratory pressures predicted by these two equations and the actual measured values among patients undergoing elective CS.
METHODS
Data Collection
This study was a retrospective design, divided into two stages that used data from 438 evaluation forms collected by the Department of Physical Therapy, Cardiopulmonary Division of Thoracic and Cardiovascular Surgery (Hospital das Clinicas; Faculty of Medicine of Ribeirão Preto - FMRP / USP) between January 2004 and December 2010. The evaluation forms contained patient assessment data from the preoperative phase and are archived in the Postoperative Unit of Thoracic and Cardiovascular Surgery. The study used data contained in the form that did not deal directly with patients or cause any potential damage or identification. For this reason, the justification for waiving the requirement of consent was approved by the research ethics committee of Hospital das Clinicas de Ribeirão Preto - FMRP / USP.
Patient Population
The study included adults of both genders aged 18 to 85 years who were undergoing elective coronary artery bypass grafting or heart valve replacement (mitral or aortic). Individuals with incomplete data, as well as those whose evaluation forms contained observations regarding the patient's difficulty in understanding the maximum effort inspiratory and/or expiratory maneuvers were excluded. Patients diagnosed with an aortic aneurysm, unstable angina or a left main coronary artery lesion, were also excluded.
First Stage - Analysis of Concordance
The first stage of the study evaluated data from 337 forms collected from January 2004 to December 2009, including 172 (51.03%) coronary artery bypass graft (CABG) patients (mean age 60.27 ± 9.80 years) and 165 (48.97%) valve replacement patients (mean age 49.72 ± 15.42 years). Of these patients, 187 (55.49%) were male and 150 (44.51%) were female.
Second Stage - Validation
The second stage of the study evaluated 101 forms collected from January 2010 to December 2010 and was aimed at validating the proposed formulas. The 101 evaluation forms included 53 (52.24%) CABG patients (mean age 53.69 ± 15.51 years for females and 62.75 ± 7.33 years for males) and 48 (47.76%) valve replacement patients (mean age 59.5 ± 7.32 years for females and 55.09 ± 16.35 years for males).
The formulas obtained in the first stage of the study were submitted to the validation process to determine the applicability of these equations in a new group.
Measurements of Maximal Respiratory Pressures
The physiotherapy team was previously trained to perform maximal static respiratory pressure measurements in a standardized method according to the guidelines for pulmonary function testing. We used an analog manometer model MV-150/300 (Ger-Ar Trade Equipamentos Ltda. São Paulo, SP, Brazil) cmH2O and graduated with a variation of ± 300 cmH2O. This manometer was fitted with an oral adapter containing a hole approximately 2 mm in diameter to avoid an increase in intraoral pressure induced by the contraction of the buccinator muscles. The method used in this study is in accordance with the recommendations of two other studies [7,8].
For the measurements, each patient was seated in a chair, so that the trunk remained at 90 degrees to the hips, and the feet were placed flat on the floor. A nose clip was used to block the upper airway (UA) during the performance of all maneuvers. First, each patient performed the maneuvers twice in order to demonstrate the proper method for the measurements; these measurements were discarded. Next, at least three reproducible maneuvers were performed, with a one-minute interval between them; measurements with a variation of more than 10% were discarded. The highest values of MIP and MEP were adopted as reference values for each patient.
Measurement of Maximal Inspiratory Pressure (MIP)
With the patient properly positioned, the measurement of MIP values was completed. The maximum static respiratory effort was assessed starting from the maximum expiration of air in the lungs, a lung volume that corresponds to the residual volume (RV). For this maneuver, a mouthpiece was connected and patients performed the maximal inspiratory effort against an occluded airway (Mueller maneuver). Acceptable maneuvers were considered those that maintained the value for at least one second [5,6,9-14].
Measurement of Maximal Expiratory Pressure (MEP)
To measure the MEP values, the patients were properly positioned, as previously described. They were instructed to inhale as much as possible until they reached the total lung capacity (TLC), and then were guided to maximum expiration through the mouthpiece, also against an occluded airway (Valsalva maneuver). As with MIP, the values were considered acceptable when they were maintained for at least one second.
Reference Values
The reference pressure values of predicted maximal static inspiratory and expiratory values were calculated from equations suggested by Black & Hyatt [5] and Neder et al. [6] as shown in Table 1.

Statistical Analysis
Statistical analysis was performed separately for each stage of the study: concordance analysis, multiple linear regression and validation. For protocol analysis, the concordance coefficients of Lin [15] and Bland & Altman plots [16] were used, and the ANOVA test was used for multiple linear regression. The coefficient proposed by Lin [15] varies between 0 and 1 and measures the degree of similarity between two instruments, using variables in continuous scale. For the Bland & Altman analysis, the ordinate axis represents the difference in measurements values and the x-axis represents the sum over 2. The same tests were applied to the validation stage. The results were obtained with the help of SAS ® 9.0 software. Results were considered significant with a P-value < 0.05.
RESULTS
First Stage - Analysis of Concordance of Maximal Static Respiratory Pressures
Maximal Inspiratory Pressure (MIP)
Figure 1 is a graphic plot of all MIP values, without any distinction of gender or age, calculated by the equations of Black & Hyatt and represented by a Bland & Altman plot and Lin's coefficient. The value of Lin's concordance coefficient (0.22) showed poor agreement when the predicted and collected values were compared.
Similarly, Figure 2 is a graphic plot of all MIP values, without any distinction of age or gender, calculated by the equations of Neder et al. and represented by a Bland-Altman plot and Lin's coefficient. The value of Lin's concordance coefficient (0.19) is also considered a weak agreement between predicted and collected values.
According to the analysis of variance (ANOVA), each relevant covariate collected this study (age, gender, weight and height) was statistically significant (P-value <0.0001) in estimating MIP. According to multiple linear regression analysis of the individual estimates of each variable (age, gender, weight and height), weight and height do not significantly affect MIP (P-level >0.05). These variables are shown in Table 2.

The linear regression model and estimated values for MIP (ANOVA) involving only the covariates with a significance level of P<0.05 (age and gender) showed statistical significance (P-value <0.0001). The estimated values for MIP were shown in Table 3.
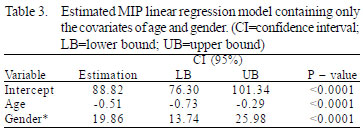
This statistical analysis allowed the creation of a new formula for calculating the MIP for patients who underwent elective CS (Figure 3).

Maximal Expiratory Pressure (MEP)
Figure 4 is a graphic plot of MEP values, without any distinction of gender or age, predicted by the equations of Black & Hyatt and represented by a Bland-Altman plot and Lin's coefficient. The value of Lin's concordance coefficient (0.10) showed poor agreement between the predicted and collected values.
Figure 5 is a graphic plot of MEP values, without any distinction of gender or age, predicted by the equations of Neder et al. and represented by a Bland-Altman plot and Lin's coefficient. The value of Lin's concordance coefficient (0.32) showed poor agreement between the predicted and collected values.
According to the ANOVA, each relevant covariates collected in this study (age, gender, weight and height) was statistically significant (P-value <0.0001) in predicting MEP.
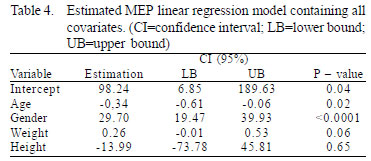
According to multiple linear regression analysis of the individual estimates of each variable (age, gender, weight and height), weight and height do not significantly affect MEP (P-value <0.05). These variables are shown in Table 4.
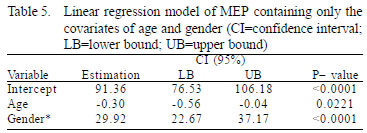
The linear regression model and estimated values for MEP (ANOVA) involving only the covariates with a significance level of P<0.05 (age and gender) showed statistical significance (P-value <0.0001). The estimated values for MEP were shown in Table 5.
This statistical analysis allowed the creation of a new formula for calculating the MEP for patients who underwent elective CS (Figure 6).

Second Stage - Validation
Maximum Inspiratory Pressure (MIP)
Figure 7 is a graphic plot of the MIP values predicted by the new formula after the ANOVA with regard to gender. Lin's concordance coefficient (0.32) demonstrated a weak correlation between the values predicted by the proposed new formula and the collected values. However, the average percentage error for calculating MIP using the new formula was 15.7% between the predicted and collected values.
Maximal Expiratory Pressure (MEP)
Figure 8 is a graphic plot of the MEP values predicted using the new formula after the ANOVA with regard to gender. Lin's concordance coefficient (0.36) demonstrated a weak correlation between the values predicted by the proposed new formula and the collected values. However, the average percentage error for calculating MEP using the new formula was 0.4% between the predicted and collected values.
DISCUSSION
The existing formulas for the evaluation of respiratory muscle strength are based on spirometry data performed in normal populations. Thus, there are controversies whether they can be applied indiscriminately in patients with respiratory disorders and/or subjected to thoracic or cardiovascular surgery, in which the surgical incisions themselves may alter the dynamics of the rib cage muscles. To test this hypothesis in patients undergoing CS, we adopted the use of two formulas: (1) the classic formula of Black and Hyatt and (2) Neder's formula, which is established as the standard for the Brazilian population. Ultimately, this research consisted of a statistical exercise in order to evaluate the suitability of two formulas to determine the respiratory muscle strength in patients scheduled for heart surgery.
All patients undergoing elective CS undergo preoperative examinations, including analysis by a physiotherapist. Thus, it is possible to identify in advance those patients with compromised respiratory muscles. And, after obtaining MIP and MEP values in the preoperative period, it is possible to engage in exercises designed to gain respiratory muscle strength. Specifically, changes in lung function in patients undergoing cardiopulmonary bypass (CPB) are primarily responsible for increasing postoperative mortality [17].
To improve outcomes concerning changes in lung function after extensive surgical procedures, it is not uncommon to control postoperative complications arising from heart surgery such as pain, arrhythmias, reduced lung volumes and capacities, and, especially, areas of atelectasis [18].
Several studies regarding maximal static respiratory pressures have been published since the pioneering study of Black 7 Hyatt [5] proposed the first formulas to calculate the MIP and MEP according to age. Measurements performed in an easy and noninvasive method show a significant correlation between the inspiratory and expiratory peaks and the strength of a patient's respiratory muscles. Differences are often found between the predicted and observed values for various ethnic groups. Such differences involve anthropometric characteristics and cultural factors and led to the proposal of new formulas in order to adjust the values of MIP and MEP for the populations in question. An extensive systematic review by Evans and Whitelaw [19] examined different formulas in the literature, in order to investigate and discuss benchmarks for the lower limit of normal, as well as the mouthpiece used in data collection. It must be emphasized that the maximal static respiratory pressures (MIP and MEP) are indirect indicators of the inspiratory and expiratory muscle strength and are essential to promote tidal volume (VT) during the ventilation process. Significant reductions in muscle strength can lead to inadequate ventilation and "clearance" of the airways [20].
For the exploratory analysis of data in the first stage of our study, we created graphical representations ("Plots") of MIP values without any distinction of gender or age. According to the values predicted by the equations of Black and Hyatt [5] and Neder et al. [6], the graphic analysis of the Plot for the formula of Black and Hyatt, and the value of Lin's concordance coefficient (0.22), there was a weak correlation between the predicted and collected values of MIP. The same occurred when graphically analyzing the Plot for the formula of Neder et al. and Lin's correlation coefficient (0.19), indicating a weak agreement (Figures 1 and 2). These reliability values observed for the MIP can be attributed to the fact that both formulas underestimated and overestimated some of the predicted values.
Studies of Black & Hyatt [5] and Neder et al. [6] evaluated only healthy individuals to establish their formulas. However, the population in this study had comorbidities that could lead to changes in the respiratory system and/or muscles and influence the values of MIP and MEP. It was evident after the first stage that the formulas of Black and Hyatt [5] and Neder et al. [6] have low sensitivity to predict values of MIP and MEP for this population of patients undergoing CS. Thus, the data were then subjected to ANOVA for MIP involving all relevant covariates collected in this study (age, gender, weight and height); each showed statistical significance level <0.0001 (Table 2). Although MIP submitted to ANOVA had a significance level of P<0.05, it was necessary to verify that all the covariates contributed significantly to the proposed model. Thus, we analyzed the independent variables and observed that weight and height did not have a significance level <0.05, and are not, in this case, relevant variables to be considered for inclusion in the multiple linear regression model.
An additional analysis was performed for MIP that involved only the covariates with a significance level <0.05 (age and gender) and the resulting model showed continued significance level <0.0001 (Table 3). In this sequence analysis, when covariates were observed individually, each had a significance level <0.0001, indicating that all the variables contributed positively to the multiple linear regression model. Evaluating the results of the ANOVA with the significance levels allowed the creation of a new formula for calculating MIP for patients undergoing elective CS: MIP = 88.82 - (0.51 x age) + (19.86 x gender [value 1 for males and 0 for females]).
Similar to the exploratory data analysis of MIP, we obtained the plot of the values of MEP without distinction of gender or age, according to the values predicted by the equations of Black & Hyatt and Neder et al. [6] (Figure 3). By analyzing the Plot graphic analysis for the MEP values from the formula of Black & Hyatt [5] and by evaluating Lin's coefficient (0.10), we observed a weak correlation between the predicted and measured MEP values (Figure 4). The same occurred when graphically analyzing the Plot for the formula of Neder et al. [6] and Lin's coefficient (0.32), indicating weak agreement between predicted and collected values.
As for the MIP, the poor similarity observed in the MEP values can also be attributed to the fact that there are underestimated and overestimated values predicted by both formulas. The ANOVA performed with data collected from MEP considered all relevant covariates (age, gender, weight and height) and identified a significance <0.0001 (Table 4). But, again, it was necessary to verify that all variables involved contributed significantly to the model, with significance level <0.05.
The analysis of individual covariates showed that height and weight did not have a significance level <0.05. In this case, the variables of weight and height were not considered relevant to the application of multiple linear regression and excluded from further analysis. Thus, a new ANOVA was performed for MEP that involved only the covariates with a significance level of P<0.05 (age and gender). The resulting model continued to show a significance level <0.0001 (Table 5). This time, however, when viewed individually, each variable showed a level of significance <0.05, demonstrating that all variables contributed significantly to the multiple linear regression model. Based on the ANOVA results, we created a new formula for calculating MEP for patients undergoing CS: MEP = 91.36 - (0.30 x age) + (29.92 x gender [value 1 for males and 0 for females]).
The second phase of research was the process of validating the proposed formulas and applying them to data obtained in 101 additional evaluation forms. In this stage, 53 (52.24%) of the patients had a surgical indication for CABG.
For exploratory data analysis to validate the formulas, a plot was again constructed from the MIP values predicted by the new formula after the ANOVA, but, this time, with respect to gender (Figure 5). According to plot graphic analysis of the MIP values and Lin's concordance coefficient (0.32), we observed a weak correlation between the MIP values predicted by the proposed new formula and the collected values. However, the average percentage error for MIP of the new formula was 15.7 % between the predicted and collected values.
As performed for MIP, a plot was obtained with the MEP values predicted by the new formula after the ANOVA, with respect to gender (Figure 6). Similar to the MIP findings, the plot for graphical analysis of the MEP values and Lin's concordance coefficient (0.36) demonstrated a weak correlation between the values predicted by the proposed new formula and the collected values. However, the average percentage error for MEP of the new formula was 0.4% between the predicted and collected values. Although the results demonstrated a poor agreement between the values predicted by the new formula and the observed population data, the percentage error is acceptable for measurements of MIP and increased for MEP. The results also showed higher values of MIP and MEP for men compared to women, which is in agreement with previous studies that found MIP for men was 34-66% greater than MIP for women and MEP was 41-57% greater for men that women, depending on age [21,22].
Age is highly correlated with the ability to generate force by skeletal muscles because, over the years, muscle strength tends to decline due to natural aging processes. Among studies of elderly patients, the values predicted by the formulas vary widely, mainly due to the small number of patients over the age of 75 years [23]. One study observed no correlation between MIP and age in the elderly [24], while at least two different studies found a strong correlation between the values of maximum static respiratory pressure and age. A large study by Carpenter et al. [25] involving 13,005 individuals aged 47 to 68 years observed a decline in MIP with older age. Yearly declines of 1.1 cmH2O for men and 0.9 cmH2O for women were observed, reaching values remarkably similar to those observed by Enright et al. [24].
When assessing respiratory muscle strength, measures of MIP and MEP may be indicators of weakness. However, the maximal static respiratory pressures only measure the combined effect of the activity of several muscles that directly or indirectly contribute to power generation for the maximum static respiratory effort. Therefore, these figures should be interpreted with caution, as some patients who have underlying disease may have MIP and MEP values near the normal range, but still develop abnormally rapid fatigue with exercise. Likewise, some patients with MIP and MEP values below the lower limits of normal can breathe perfectly well without any difficulties. The classification of respiratory muscle weakness should not be solely based on the individual values of MIP and MEP.
Also important to note is that all previously published studies were based on healthy patients without any previous illnesses or comorbidities. The patients in this study could present insufficient pulmonary respiratory mechanics, reduced lung volumes and chest expansion, and/or possible altered diaphragmatic excursion, as observed in previous studies [22,23].
Study limitation
Owing to the fact that it was a retrospective analysis, with data collected during from January 2004 to December 2010, it was not possible for a single professional to collect data from the evaluation forms at the time of the patient hospitalization. Clinical problems as renal failure, hypertension, tabagism and obstructive lung disease, which are frequent were not considered for exclusion criteria because they have relatively high incidence in adult patients under cardiac surgery. However, this option would be considered for criticism.
CONCLUSIONS
This study reaches two main conclusions: 1) Neither Black and Hyatt's nor Neder et al.'s formula reach complete agreement between predicted and observed maximal static respiratory pressure values in patients undergoing CS, and 2) the proposed new formulas have a low percentage error (15.7% for MIP and 0.4% for MEP) and are, therefore, more appropriate when used for a population of patients undergoing CS.
Support Statement
This study was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Fundação de Apoio ao Ensino, Pesquisa e Assistência do Hospital das Clínicas da Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo (FAEPA/HCFMRP/USP), SP, Brazil.
Statement of Interest
None declared.
ACKNOWLEDGEMENTS
The authors would like to thank the patients, physicians and physiotherapists from the Division of Thoracic and Cardiovascular Surgery.
REFERENCES
1. Sarmento GJV. Fisioterapia hospitalar: pré e pós-operatórios. São Paulo: Manole; 2008. p.37.
2. Yánez-Brage I, Pita-Fernández S, Juffé-Stein A, Martínez-González U, Pértega-Díaz S, Mauleón-García A. Respiratory physiotherapy and incidence of pulmonary complications in off-pump coronary artery bypass graft surgery: an observational follow-up study. BMC Pulm Med. 2009;9:36. [MedLine]
3. Herdy AH, Marcchi PL, Vila A, Tavares C, Collaço J, Niebauer J, et al. Pre- and postoperative cardiopulmonary rehabilitation in hospitalized patients undergoing coronary artery bypass surgery: a randomized controlled trial. Am J Phys Med Rehabil. 2008;87(9):714-9. [MedLine]
4. Garcia RCP, Costa D. Treinamento muscular respiratório em pós-operatório de cirurgia cardíaca eletiva. Rev Bras Fisioter. 2002;6(3):139-46.
5. Black LF, Hyatt RE. Maximal respiratory pressures: normal values and relationship to age and sex. Am Rev Respir Dis. 1969;99(5):696-702. [MedLine]
6. Neder JA, Andreoni S, Lerario MC, Nery LE. Reference values for lung function tests. II. Maximal respiratory pressures and voluntary ventilation. Braz J Med Biol Res. 1999;32(6):719-27. [MedLine]
7. Camelo Jr JS, Terra JT, Manço JC. Pressões respiratórias máximas em adultos normais. J Pneumol. 1985;11(4):181-4.
8. Sobush DC, Dunning M 3rd. Assessing maximal static ventilatory muscle pressures using the "bugle" dynamometer. Suggestion from the field. Phys Ther. 1984;64(11):1689-90. [MedLine]
9. Vincken W, Ghezzo H, Cosio MG. Maximal static respiratory pressures in adults: normal values and their relationship to determinants of respiratory function. Bull Eur Physiopathol Respir. 1987;23(5):435-9. [MedLine]
10. Bruschi C, Cerveri I, Zoia MC, Fanfulla F, Fiorentini M, Casali L, et al. Reference values of maximal respiratory mouth pressures: a population-based study. Am Rev Respir Dis. 1992;146(3):790-3. [MedLine]
11. Fiz JA, Carreras A, Aguilar J, Gallego M, Morera J. Effect of order on the performance of maximal inspiratory and expiratory pressures. Respiration. 1992;59(5):288-90. [MedLine]
12. Wilson SH, Cooke NT, Edwards RH, Spiro SG. Predicted normal values for maximal respiratory pressures in Caucasian adults and children. Thorax. 1984;39(7):535-8. [MedLine]
13. Wagener JS, Hibbert ME, Landau LI. Maximal respiratory pressures in children. Am Rev Respir Dis. 1984;129(5):873-5. [MedLine]
14. McElvaney G, Blackie S, Morrison NJ, Wilcox PG, Fairbarn MS, Pardy RL. Maximal static respiratory pressures in the normal elderly. Am Rev Respir Dis. 1989;139(1):277-81. [MedLine]
15. Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45(1):255-68. [MedLine]
16. Bland JM, Altman DG. Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet. 1995;346(8982):1085-7. [MedLine]
17. Johnson D, Hurst T, Thomson D, Mycyk T, Burbridge B, To T, et al. Respiratory function after cardiac surgery. J Cardiothorac Vasc Anesth. 1996;10(5):571-7. [MedLine]
18. Hayes JP, Williams EA, Goldstraw P, Evans TW. Lung injury in patients following thoracotomy. Thorax. 1995;50(9):990-1. [MedLine]
19. Evans JA, Whitelaw WA. The assessment of maximal respiratory mouth pressures in adults. Respir Care. 2009;54(10):1348-59. [MedLine]
20. Berry JK, Vitalo CA, Larson JL, Patel M, Kim MJ. Respiratory muscle strength in older adults. Nurs Res. 1996;45(3):154-9. [MedLine]
21. Hautmann H, Hefele S, Schotten K, Huber RM. Maximal inspiratory mouth pressures (PIMAX) in healthy subjects: what is the lower limit of normal? Respir Med. 2000;94(7):689-93. [MedLine]
22. Harik-Khan RI, Wise RA, Fozard JL. Determinants of maximal inspiratory pressure. The Baltimore Longitudinal Study of Aging. Am J Respir Crit Care Med. 1998;158(5 Pt 1):1459-64. [MedLine]
23. Watsford ML, Murphy AJ, Pine MJ, Coutts AJ. The effect of habitual exercise on respiratory- muscle function in older adults. J Aging Phys Act. 2005;13(1):34-44. [MedLine]
24. Enright PL, Kronmal RA, Manolio TA, Schenker MB, Hyatt RE. Respiratory muscle strength in the elderly. Correlates and reference values. Cardiovascular Health Study Research Group. Am J Respir Crit Care Med. 1994;149(2 Pt 1):430-8. [MedLine]
25. Carpenter MA, Tockman MS, Hutchinson RG, Davis CE, Heiss G. Demographic and anthropometric correlates of maximum inspiratory pressure: The Atherosclerosis Risk in Communities Study. Am J Respir Crit Care Med. 1999;159(2):415-22. [MedLine]
This study was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Fundação de Apoio ao Ensino, Pesquisa e Assistência do Hospital das Clínicas da Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo (FAEPA/HCFMRP/USP), SP, Brazil.
Article receive on Thursday, December 22, 2011
 All scientific articles published at rbccv.org.br are licensed under a Creative Commons license
All scientific articles published at rbccv.org.br are licensed under a Creative Commons license